Different Types of Triangles: Definition, Characteristics, Shapes, & Real-life Application

If we talk about triangles, we all are aware of them as a shape, but do you all remember what the different characteristics, actual definitions, and real-life applications of triangles are? Do you remember how many types of triangles are there? In case you do not remember, then after reading this blog, you will get a clear picture of triangles as a whole.

When we define a triangle, it is a closed polygon having three sides that are equal and unequal. If we talk about how a triangle is made, it consists of three sides, three vertexes, and three angles, which can or cannot be the same. Therefore, a triangle is divided on the basis of angles and sides; we will discuss it later. 

Firstly, we will discuss the essentials of triangles: vertex and angles. 

The point where the two straight lines are known as the vertex. 

The angle is produced between the two sides. As a part of geometry, the triangle plays a crucial role in developing the fundamentals of mathematics. 

Triangle features, like the Pythagorean theorem and trigonometry, are essential to certain fundamental ideas.

Furthermore, a triangle generally consists of three sides that connect each other. The length of each side might be the same as well as might be different, but it is also not possible that the longest side of a triangle is greater or equal to the other sides. 

In addition, it is also true that a triangle has three internal and exterior angles. Combining these three interior angles always sums up to 180 degrees, and the same goes for exterior angles, as their sum is also 180 degrees.

The shape of Triangle

A closed, two-dimensional shape is a triangle. It is a polygon with three sides. All sides of the triangle are made up of straight lines. The intersection of two straight lines forms a vertex. And do you know that a triangle has its vertices, and each vertices combined forms an angle?

Angles of Triangle

A triangle consists of three angles. And the triangle's two sides meet at the triangle's vertices to produce these angles. When we add the three inner angles of a triangle, then it is always 180 degrees.

If we stretch out the triangle outside, then the side length of the triangle creates an angle. The total of a triangle's contiguous interior and exterior angles is supplementary.

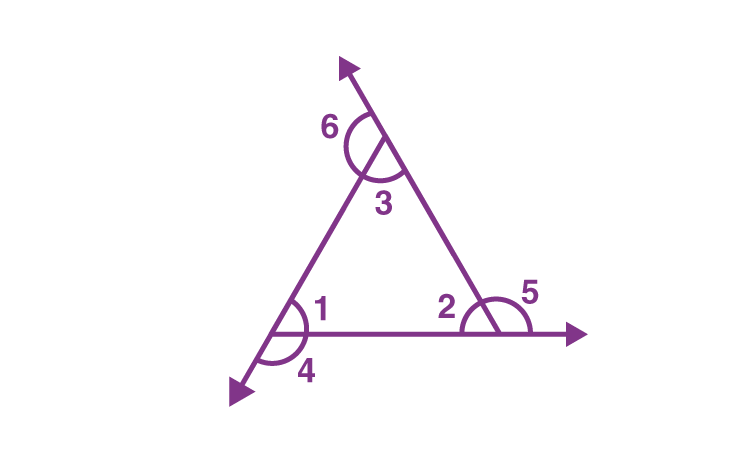
Let's assume that the internal angles of a triangle are ∠1, ∠2, and ∠3. The three external angles that are created when the triangle's sides are extended outward are ∠4, ∠5, and ∠6, and they follow each other in the order of ∠1, ∠2, and ∠3, respectively.

Hence,

∠1 + ∠4 = 180°   ……(i)

∠2 + ∠5 = 180°  …...(ii)

∠3 + ∠6 = 180° ….(iii)

If we add the above three equations, we get.

∠1+∠2+∠3+∠4+∠5+∠6 = 180° + 180° + 180°

Now, by angle sum property, we know,

∠1+∠2+∠3 = 180°

Therefore,

180 + ∠4+∠5+∠6 = 180° + 180° + 180°

∠4+∠5+∠6 = 360°

Thus, the triangle's outside angles add up to 360 degrees, as inclinations by the equation above.

Characteristics of the Triangle

There are some characteristics that set each and every form of mathematics apart. Let's talk about a few triangle qualities now. 

1. A triangle consists of three angles and three sides.
2. When we add up all the angles of a triangle, it always equals 180 degrees.
3. Any triangles’ outside angles add up to 360 degrees every time.
4. The sum of each exterior and interior angle equals 180 or supplements to each other.
5. The third side of any triangle is always shorter than the sum of the lengths of the other two sides. In the same way, the difference in length between any two of a triangle's sides is always smaller than the difference in length between the third side.
6. In every triangle, the shortest side is always opposite the smallest angle inside the triangle. Likewise, the longest side is always across from the largest angle inside the triangle.

Different Types of Triangles

Since a triangle is a closed figure, it may take on several forms, and the angle formed by any two of its sides describes a shape. Now, let's explore the various kinds of triangles.

But the question is how would one determine which type of triangle is it? Check the largest angle in each triangle and see if it is more than, less than, or equal to 90 degrees.  Still, if you are confused about how to identify each one, do not worry, we are here to help you out. Just search for “Do my Assignment” and connect with us. We have a team of highly competent experts who are here to aid you in understanding this concept. Our Experts have years of experience in providing assignment help successfully to students.

What is an Acute Angle Triangle?

An acute-angled triangle, a fundamental geometric shape, is defined by its interior angles, each of which measures less than 90 degrees. This type of triangle showcases a characteristic in which all three angles are acute, contributing to the sum of the interior angles amounting to 180 degrees. As a result, the sides of the acute-angled triangle are shorter than those of other types, demonstrating a balanced distribution of angles that allows for a visually compact and pointed structure.

Important characteristics of an acute triangle:

Let's know what the important characteristics of this type of triangle are.

• Every internal angle of an acute triangle is less than ninety degrees, and the lengths of the sides vary.

• An acute triangle also has the fascinating property that any line drawn from its base to its opposite corner will always be perpendicular to the base.

What is a Right-Angled Triangle?

A right-angled triangle, often referred to as a right triangle or a 90-degree triangle, is a type of triangle where one of its interior angles measures exactly 90 degrees. This triangle holds significance in the field of trigonometry.

Characterizes of Right-Angle Triangle

Once you are familiar with the definition, it's time for you to give your attention to the various characteristics of a right-angle triangle.

• Only one angle is a 90° angle, or a right angle in this type of triangle.
• The hypotenuse, which is the longest side, is always in opposition to the 90° angle.
• The sum of two angles that are apart from 90 degrees is 90 degrees.
• The sides that are adjacent to 90-degree angle are called perpendicular and base of triangle.
• A right-angle triangle's area is equal to half of (base x perpendicular).
• When a line is drawn from the right angle to the hypotenuse, it creates three similar triangles.
• A circle passing through all three corners has a radius half the length of the hypotenuse.

Shape of Right Triangle

Now, the question arises, what are the shapes of right-angle triangles? Three sides enclose together to form a right-angle triangle, out of which one side is straight and is known as the height or leg of this type of triangle.

What is an obtuse angle?

An obtuse triangle is a triangle whose angle is more than ninety degrees. It is sometimes referred to as an obtuse-angled triangle.  But as it stated that the sum of all interior angles of a triangle is always 180 degrees, the same goes for this triangle. The entire sum of the internal angles of an obtuse triangle is still 180 degrees. This angle type is important in math and shapes, helping us understand how different angles and shapes relate to each other.

As a result, two additional angles in the triangle must be acute, meaning they are both fewer than ninety degrees if one angle in the triangle is obtuse (greater than ninety degrees).

Characteristics of Obtuse Angled Triangle

Have a glimpse of the various characteristics of the Obtuse Angled Triangle.

1. The sum of the two angles, excluding the obtuse angle, is less than ninety degrees.
2. The longest side of the triangle is opposite the obtuse angle.
3. An obtuse triangle is characterized by a single obtuse angle, with the remaining two acute angles.
4. The point where all the perpendicular bisectors drawn from each side meets is the circumcenter, and this circumcenter, in the case of an obtuse-angled triangle, meets outside the triangle.
5. The points of concurrency—the Circumcenter and the Orthocenter—are positioned outwards the obtuse triangle, whereas the Centroid and Incenter are inwards the triangle.

What is an Equilateral Triangle?

In geometry, when you talk about equilateral triangles, this type of triangle has equal sides, which results in the angles that are opposite to these sides being equal. This property deduces the conclusion that each angle of an equiangular triangle seems to be 60 degrees.

In line with the angle sum property of triangles, the total of all three angles in an equilateral triangle amounts to 180 degrees (60° + 60° + 60° = 180°). Similar to other types of triangles, the equilateral triangle possesses its own set of formulas for area, perimeter, and height, which can be explored in greater detail.

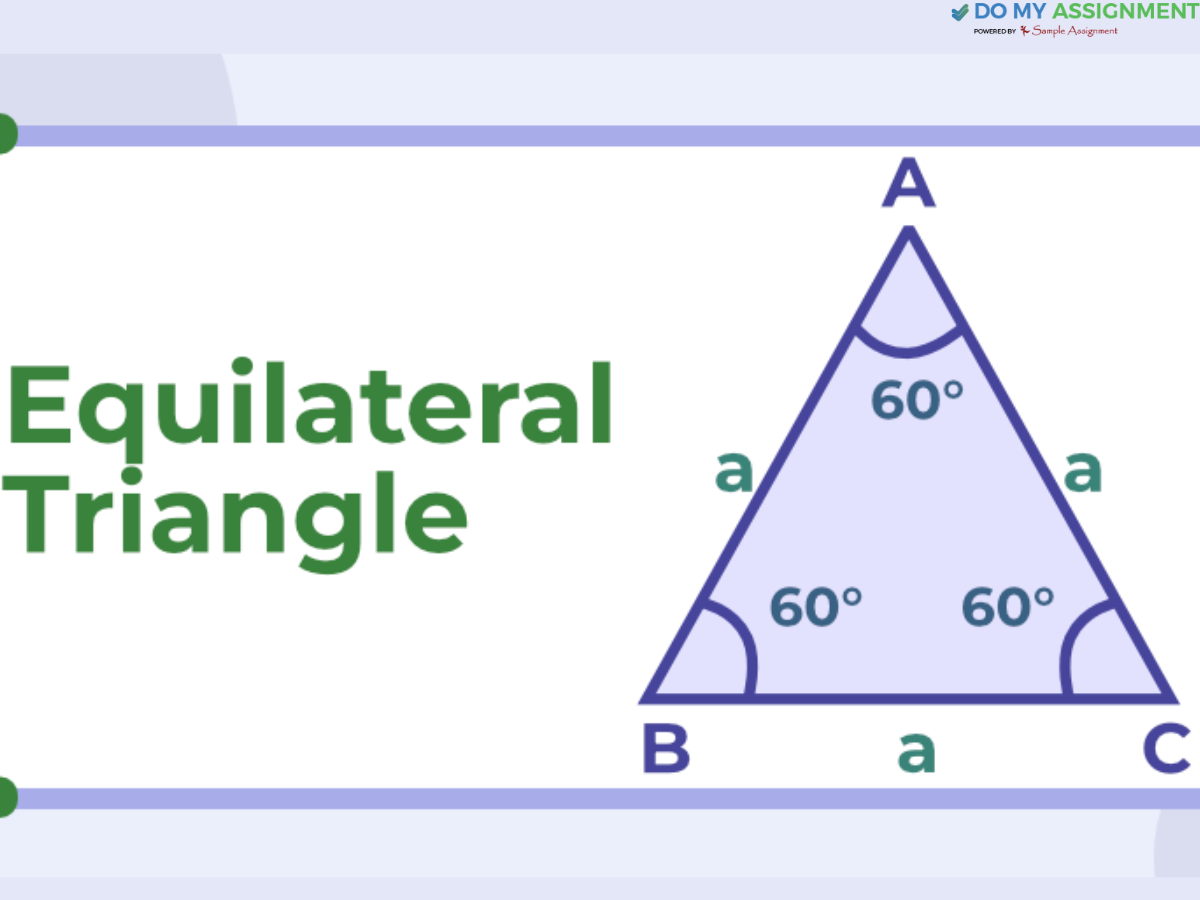
Characteristics of Equilateral Triangle

Get a hand on the various characteristics of an equilateral triangle.

• All three sides are of equal length.
• All three angles are the same, each measuring 60 degrees.
• It's a three-sided shape known as a regular polygon.
• Drawing a line from any corner to the opposite side splits the angle into two equal parts, each measuring 30 degrees.
• The point where the lines intersect is both the center of gravity and the intersection of the altitudes.
• This triangle consists of a median, angle bisector, and altitude, indicating that all sides are the same length.
• The area of the equilateral triangle is (√3a) / 4, where 'a' is the length of one side.
• The perimeter of an equilateral triangle is a multiple of 3 of its one side.

Shape of Equilateral Triangle

When we talked about the shape of this type of triangle, it is regular in nature. Moreover, the term equilateral is derived from the combination of two words that is “equi’, which means equal, and “Lateral,” which means sides.

A regular polygon has all its sides equal. If we are talking about an equilateral triangle, then it also has all three sides equal. Hence, an equilateral triangle is basically a type of regular polygon having all three sides equal.

Let's assume that ABC is an equilateral triangle having AB, BC, and AC as their sides; so, as per the definition, each side of the triangle is equal. This means that.

AB = BC = AC

And

∠A = ∠B = ∠C = 60°

What is the Isosceles Triangle?

An isosceles triangle is a triangle in which the two sides are the same length. It means that in this kind of triangle, the two angles facing these equal sides are also the same. So, if you have a triangle ABC, and sides AB and AC are equal, then you have an isosceles triangle, and it also means that angle B is equal to angle C. A theorem describes this idea: if two sides of a triangle are the same length, then the angles across from them are also the same.

Characteristics of Isosceles Triangle

 Here are the characteristics of the isosceles triangle through which you will get more clarity about this type of triangle.

1. As discussed above, the two sides of this triangle are equal, and the unequal side is, therefore, known as the triangle's base.
2. As the two sides of this triangle are equal, therefore, the opposite angles to these sides are always equal.
3.  The altitude of this triangle is measured, or we can say drawn from the unequal side, which is the triangle base to the topmost vertex of the triangle.
4. Another triangle is called a right-angled triangle, has two equal angles, and the third one equals 90 degrees.

Types of Isosceles Triangle

Generally, the isosceles triangle is classified into different types, namely:

Isosceles Acute Triangle:

Isosceles triangles have a line of symmetry along the perpendicular bisector of their base. Depending on the angle formed between the two equal-length legs, they can be classified as acute, right, or obtuse. An isosceles triangle is considered acute when the two angles opposite the sides are equal and less than 90 degrees.

Isosceles Right Triangle:

In a right isosceles triangle, two sides are of equal length, with one serving as the perpendicular side and the other as the base. The third side, which is unequal, is referred to as the hypotenuse. This triangle obeys the Pythagoras theorem, where the square of the hypotenuse equals the sum of the squares of the base and perpendicular sides. If the lengths of the equal sides are 'a' and the hypotenuse is 'h,' then h = √2a or h = a√2.

Isosceles Obtuse Triangle:

An obtuse triangle is one in which at least one of its angles exceeds 90 degrees (a right angle). Triangles with more than one obtuse angle cannot exist. An isosceles obtuse triangle is a specific case where two sides are of equal length, and one angle is obtuse.

Isosceles Triangle Theorem

This theorem is very well known in mathematics, and it basically explains one of the most important properties of the isosceles triangle if two sides of this triangle are equal or congruent to each other, then the angles opposite to these sides are also congruent or equal.

This theorem can also be alternately seen as that if two angles of an isosceles are congruent to each other, then the sides opposite to them will also be congruent to each other.

In the above triangle ABC,

Sides AB is equal to AC.

Angle ABC is equal to the angle ACB.

What is a Scalene Triangle?

Last, if we talk about the scalene triangle, is a type of triangle in which none of its sides are equal to each other, which states that there are no angles in this triangle that are equal to each other.

A scalene triangle is a type of triangle where all three sides have different lengths, and all three angles have different measures. Nevertheless, the sum of all the interior angles always equals 180 degrees, adhering to the fundamental angle sum property of any triangle.

Characteristics of Scalene Triangle

After definition it is time to learn what are the various characteristics of the scalene triangle.

• All sides have different lengths, with none being equal.
• Each angle has a distinct measure, with no two being equal.
• It lacks any lines of symmetry and point symmetry.
• Its interior angles can be acute, obtuse, or right angles.
• When all angles are acute, the circumscribing circle's center is inside the triangle.
• In a scalene obtuse triangle, the circumcenter is outside the triangle.
• It can be an acute-angled, obtuse-angled, or right-angled triangle.

Types of Scalene Triangles:

Learn the several types of scalene triangles to have more in-depth knowledge about this type of triangle.

• Acute scalene triangle: The Circumcenter lies within the triangle.
• Obtuse Scalene Triangle: The Circumcenter is positioned outside the triangle.
• Right-angled Scalene Triangle: Circumcenter is at the midpoint of the hypotenuse.

Real-Life Applications of Different Types of Triangles

We have heard about these triangles in our school life, but do you remember what their uses are?  No worries if you are not familiar with this. Just keep reading to learn about the real-life uses of triangles.

So, if you are concerned about that you may get this type of question in your assessment. But you have no proper knowledge about this. Do not worry, we are here to aid you offering the best “assessment help” Services so that you can boost your knowledge accordingly.

Furthermore, Triangles are fundamental geometric shapes, and their applications extend to various aspects of daily life and numerous fields, such as architecture, engineering, and science. Here are real-life applications of different types of triangles:

Equilateral Triangle:

• Trusses: Equilateral triangles are used in building trusses and frameworks, providing stability and support in structures like bridges and roofs.
• Road Signs: Triangle-shaped Road signs use equilateral triangles to draw attention and convey important information to drivers.

Isosceles Triangle:

• Pyramids: The faces of a pyramid are often isosceles triangles, as seen in the pyramids of Egypt. These structures have been used historically as tombs and monuments.
• Bridges: Some cable-stayed and suspension bridges use isosceles triangles in their support structures to distribute weight effectively.

Scalene Triangle:

• Surveying: Surveyors use scalene triangles to measure distances and calculate land areas, ensuring accurate property boundaries and land development.
• Aircraft Design: In the aerospace industry, scalene triangles are employed to create the shape of wings, tail fins, and other components to optimize aerodynamics.

Right Triangle:

• Carpentry: To guarantee square corners and level, plumb buildings, right triangles are essential.
• Trigonometry: The study of right triangles is fundamental to trigonometry, which is used in construction, navigation, and the resolution of practical angle and distance issues.

Acute Triangle:

• Art and Design: Acute triangles are utilized in art and design to produce dynamic compositions and designs that have a sense of energy and equilibrium.
• Mechanical Engineering: When developing mechanical parts, where exact angles and dimensions are required for effective functioning, acute triangles are used.

Obtuse Triangle:

• Geodetic surveying and obtuse triangles may be seen in the process of calculating locations, angles, and distances on the surface of the Earth.
• Navigation: Obtuse triangles are employed in computations for navigational purposes, such as figuring out the positions of celestial bodies.

Isosceles Right Triangle:

• Construction: To ensure that buildings and other structures are constructed with precise angles and dimensions, isosceles right triangles are used to establish and verify right angles.
• Cable Installation: In electrical and telecommunications operations, these triangles assist in installing cables and wires at right angles to walls and buildings.

To create stable and aesthetically pleasing designs, solve real-world problems, and maintain accuracy in various applications, architects, engineers, artists, and many other professionals need to understand the various types of triangles and their properties.

Wrapping Up

In summary, knowledge of the numerous triangle types—equilateral, isosceles, scalene, right-angled, acute, and obtuse—lays the groundwork for comprehending their special qualities and uses in various contexts. Triangles with equal sides stand for harmony and balance, whereas those with an odd number of sides emphasise stability and symmetry.

Scalene triangles are known for their adaptability and usefulness, but right-angled triangles are fundamental to the Pythagorean theorem and other geometric concepts. The distinction between acute and obtuse triangles draws attention to the various angles and their use in practical situations.

Understanding the importance of each triangle form allows us to apply this knowledge to various industries, from mathematics and art to architecture and engineering, encouraging creativity and problem-solving across the board.

So, if you are interested in knowing more about this, you can visit audomyassignment.com and search “do my maths homework”. Once you finish this, you will connect with our highly skilled experts who hold Ph.D. degrees in mathematics and are eager to help you. So, why hold back? Connect with us now!